Grafos

Grafos

Grafo (estructura de dat

Un grafo en el ámbito de las ciencias de la computación es una estructura de datos, en concreto un tipo abstracto de datos (TAD), que consiste en un conjunto de nodos (también llamados vértices) y un conjunto de arcos (aristas) que establecen relaciones entre los nodos. El concepto degrafo TAD desciende directamente del concepto matemático de grafo.

Informalmente se define como G = (V, E), siendo los elementos de V los vértices, y los elementos de E, las aristas (edges en inglés). Formalmente, un grafo, G, se define como un par ordenado, G = (V, E), donde V es un conjunto finito y E es un conjunto que consta de dos elementos de V.

En teoría de grafos, un vértice o nodo es la unidad fundamental de la que están formados los grafos. Un grafo no dirigido está formado por un conjunto de vértices y un conjunto de aristas (pares no ordenados de vértices), mientras que un grafo dirigido está compuesto por un conjunto de vértices y un conjunto de arcos (pares ordenados de vértices). En este contexto, los vértices son tratados como objetos indivisibles y sin propiedades, aunque puedan tener una estructura adicional dependiendo de la aplicación por la cual se usa el grafo; por ejemplo, una red semántica es un grafo en donde los vértices representan conceptos o clases de objetos.

Los dos vértices que conforman una arista se llaman puntos finales ("endpoints", en inglés), y esa arista se dice que es incidente a los vértices. Un vértice w es adyacente a otro vértice v si el grafo contiene una arista (v,w) que los une. La vecindad de un vértice v es un grafo inducido del grafo, formado por todos los vértices adyacentes a v.

En Teoría de grafos, las aristas, junto con los vértices, forman los elementos principales con los que trabaja esta disciplina, siendo consideradas las aristas las uniones entre nudos o vértices.

Existen diferentes implementaciones del tipo grafo: con una matriz de adyacencias (forma acotada) y con listas y multilistas de adyacencia (no acotadas).

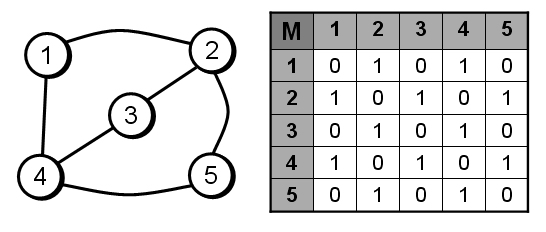
• Matriz de adyacencias: se asocia cada fila y cada columna a cada nodo del grafo, siendo los elementos de la matriz la relación entre los mismos, tomando los valores de 1 si existe la arista y 0 en caso contrario.

• Lista de adyacencias: se asocia a cada nodo del grafo una lista que contenga todos aquellos nodos que sean adyacentes a él.

Especificación de los tipos abstractos de datos de un grafo no dirigido

Generadores

Crear un grafo vacío: Devuelve un grafo vacío.

• op crearGrafo : -> Grafo [ctor] .

Añadir una arista: Dado un grafo, añade una relación entre dos nodos de dicho grafo.

• op añadirArista : Grafo Nodo Nodo -> [Grafo] [ctor] .

Añadir un nodo: Dado un grafo, incluye un nodo en el en caso en el que no exista previamente.

• op añadirNodo : Grafo Nodo -> Grafo [ctor] .

Constructores

Borrar nodo: Devuelve un grafo sin un nodo y las aristas relacionadas con él. Si dicho nodo no existe se devuelve el grafo inicial.

• op borrarNodo : Grafo Nodo -> Grafo .

Borrar arista: Devuelve un grafo sin la arista indicada. En caso de que la arista no exista devuelve el grafo inicial.

• op borrarArista : Grafo Nodo Nodo -> Grafo .

Grafo Vacio: Comprueba si un grafo no tiene ningún nodo.

• op esVacio : Grafo -> Bool .

Contener Nodo: Comprueba si un nodo pertenece a un grafo.

• op contiene : Grafo Nodo -> Bool .

Adyacentes: Comprueba si dos nodos tienen una arista que los relacione.

• op adyacentes : Grafo Nodo Nodo -> Bool .

Para la especificación de un grafo dirigido tenemos que modificar algunas de las ecuaciones de las operaciones borrarArista y añadirArista para que no se considere el caso de aristas bidireccionales.